Ketika makanan dipaparkan ke temperatur dingin, produk makanan tersebut akan kehilangan panas akibat laju pindah panas yang terjadi dari makanan ke medium bertemperatur rendah di sekitarnya. Permukaan makanan akan mengalami penurunan temperatur lebih cepat dibandingkan dengan bagian dalamnya. Jumlah air yang membeku dalam produk makanan tergantung pada temperatur pembekuan; kandungan campuran zat makanan amat memengaruhi hal tersebut. Umumnya, semakin cair suatu bahan makanan, jumlah air yang membeku akan semakin banyak. Tetapi, kuning telur masih menyisakan lebih dari 20 persen air meski sudah didinginkan hingga minus 40oC. Hal ini dikarenakan kandungan protein yang tinggi yang terlarut dalam air. Kekurangan teknik pembekuan adalah sulitnya membekukan kandungan air yang ada dalam bahan makanan secara sempurna sehingga masih menyisakan risiko pertumbuhan mikroorganisme; untuk mengatasinya diperlukan pendinginan lebih jauh lagi untuk menghentikan aktivitas enzim mikroorganisme dan/atau membekukan lebih banyak air, namun hal itu tidaklah ekonomis.
Prinsip dari proses pembekuan suatu bahan adalah penurunan suhu bahan tersebut sampai dibawah titik bekunya, sehingga air dalam bahan akan membeku. Dari termodinamika telah diketahui bahwa penurunan suhu merupakan suatu pengambilan energi dalam bentuk panas, oleh karena itu dasar-dasar pindah panas harus diketahui untuk dapat menduga berapa besar panas yang harus dipindahkan hingga tujuan pembekuan dapat dicapai. Secara umum, semakin besar laju pemindahan panas maka semakin cepat proses pembekuan tercapai, akan tetapi tanpa perhitungan yang memadai proses yang optimal tidak dapat dipenuhi. Beberapa pendugaan waktu pembekuan yang didasarkan pada pindah panas telah berkembang diantaranya mencakup persamaan Plank, Neumann dan lain-lain (Heldman and Singh, 1981).
Persamaan Plank
Ekspresi untuk perhitungan waktu pembekuan telah diturunkan oleh Plank. Persamaan ini berguna untuk menghitung berbagai bentuk geometri produk. Pada Gambar 1 dilukiskan perhitungan pembekuan untuk bentuk lempeng satu dimensi. Tiga persamaan dasar digunakan dalam penurunan persamaan perhitungan waktu ini. Persamaan yang digunakan adalah persamaan konduksi panas untuk daerah beku:
 ............................................................................................................(12-6)
............................................................................................................(12-6)
dimana Tf titik beku awal dan mewakili suhu seluruh daerah yang tidak beku.
Persamaan yang kedua adalah pindah panas pada permukaan bahan dengan lingkungan secara konvektif yang diekspresikan ke dalam persamaan berikut:
 ................................................................................................(12-7)
................................................................................................(12-7)
Kombinasi kedua persamaan diatas adalah sebagai berikut:
 .............................................................................................(12-8)
.............................................................................................(12-8)
Persamaan yang ketiga merupakan laju pembentukan panas pada front pembekuan yang merupakan efek perubahan fase, yaitu:
 .........................................................................................................(12-9)
.........................................................................................................(12-9)
dimana L merupakan panas laten pembekuan.
Dengan menyamakan persamaan 12-9 dan 12-10, maka dapat ditulis sebagai berikut
 ..............................................................................................(12-10)
..............................................................................................(12-10)
Integrasi dari persamaan diatas dari 0 sampai ketebalan ½ a adalah
 ........................................................................................(12-11)
........................................................................................(12-11)
dengan memasukkan nilai tersebut dan mengubah posisi, maka persamaan diatas dapat ditulis sebagai:
 ..........................................................................................................(12-12)
..........................................................................................................(12-12)
Persamaan diatas dapat berlaku umum untuk bentuk geometri yang lain, dengan menggantikan nilai ½ dan 1/8 dengan konstanta P dan R. Konstanta P dan R ini mempunyai nilai sebagai berikut:
• untuk bola P=1/6 dan R = 1/24
• untuk silinder tak berhingga P = 1/4 dan R = 1/16
dimana a merupakan diameter dari bola / silinder.
Penggunaan persamaan Plank terbatas karena alasan-alasan sebagai berikut:
• Asumsi panas laten tidak mempertimbangkan pemindahan panas laten secara gradual pada selang suhu selama proses pembekuan.
• Harga menggunakan titik beku awal dalam perhitungan persamaan dan mengabaikan kebutuhan waktu untuk pemindahan panas sensibel di atas titik beku.
• K diasumsikan konstan untuk daerah beku, sedangkan seharusnya k berubah sejalan dengan perubahan suhu dengan daerah beku.
Masalah Neumann
Pada pemecahan ini, pendekatan dilakukan dengan menggunakan pindah panas satu dimensi untuk benda yang semi tak hingga. Pertimbangan untuk kedua fase ( cair dan beku) dimasukkan, oleh karena itu dua persamaan parsial digunakan yaitu:
 ...............................................................................................(12-13)
...............................................................................................(12-13)
 ...............................................................................................(12-14)
...............................................................................................(12-14)
Selain itu, perbedaan panas antara porsi padatan dengan porsi cairan harus sama dengan panas pada front pembekuan, yang ekspresinya dinyatakan sebagai berikut:
 ......................................................................................(12-15)
......................................................................................(12-15)
Dengan menggunakan kondisi awal dan kondisi batas sebagai berikut:
Pada x(t) : T1 = T2 = TF
Pada x - ~ : T2 = TI
Pada x = 0,t > 0 : T1 = 0
Pada x(t) = 0 : T2 = T1
Dengan demikian pemecahan persamaan dan persamaan dapat ditulis sebagai berikut:
 ..................................................................................................(12-16)
..................................................................................................(12-16)
 ...........................................................................(12-17)
...........................................................................(12-17)
dimana l merupakan suatu konstanta yang harus dievaluasi secara trial dan error. Perhitungan diatas cukup kompleks dan mencakup masalah trial dan error, sehingga sering dihindari, dengan demikian apabila memungkinkan, penggunaan persamaan yang lebih sederhana lebih digunakan.
Perhitungan kebutuhan total waktu untuk pembekuan tidak terlepas dari waktu pre-freezing/cooling dari suhu awal ke suhu di atas titik beku. Terdapat tiga metode yang didasarkan pada asumsi yang berbeda dalam perhitungan yang berbeda:
• Perhitungan dengan mengabaikan tahanan dalam (internal)
• Perhitungan dengan mengabaikan tahanan permukaan
• Perhitungan dengan memperhitungkan keduanya.
Untuk lebih jelasnya diuraikan di bawah ini.
a. Perhitungan dengan mengabaikan tahanan dalam (internal)
Pada situasi ini, diasumsikan bahwa tahanan permukaan jauh lebih besar daripada tahanan intrernal. Dengan demikian suhu permukaan ini adalah seragam. Untuk suatu objek, keseimbangan energi dapat dinyatakan sebagai berikut:
 ................................................................................................................................(12-18)
................................................................................................................................(12-18)
 .......................................................................................................................................(12-19)
.......................................................................................................................................(12-19)
 ................................................................................................................................(12-20)
................................................................................................................................(12-20)
Dengan mengekspresikan bentuk diatas dalam bilangan tak berdimensi, maka:
 ...................................................................................................................................(12-21)
...................................................................................................................................(12-21)
dimana  dan
dan 
b. Perhitungan dengan mengabaikan tahanan permukaan
Perhitungan ini didasarkan panda asumsi tahanan internal yang jauh lebih besar daripada tahanan produk. Ini mengakibatkan laju pendinginan produk sangat ditentukan oleh jenis produk, selain geometri produk juga merupakan faktor yang mempengaruhi.
Ekpresi dikembangkan dari persamaan energi dalam suatu sistem, yang dalam bentuk satu dimensi bentuk lempeng dinyatakan sebagai berikut:
 .............................................................................................................(12-22)
.............................................................................................................(12-22)
Pemecahan dari persamaan diatas adalah sebagai berikut:
 .............................................................................(12-23)
.............................................................................(12-23)
Pemecahan juga telah dilakukan untuk bentuk silinder dan bola, yang masing-masing ditunjukkan pada persamaan berikut:
Bentuk silinder tak-hingga :
 .................................................................................(12-24)
.................................................................................(12-24)
Bentuk bola :
 .....................................................................(12-25)
.....................................................................(12-25)
• Perhitungan dengan memperhitungkan tahanan internal dan permukaan
Perhitungan dengan asumsi ini digunakan apabila nilai bilangan Biot berada pada 0.1 sampai 40. Nilai bilangan ini menyiratkan bahwa kedua tahanan, baik internal maupun permukaan mempunyai besar yang cukup berarti, sehingga perhitungan dilakukan dengan mencakup kedua tahanan tersebut. Untuk maksud tersebut, digunakan bagan yang mempermudah dalam perhitungan pindah panas.
• Perpindahan Uap Air
Migrasi uap air adalah perubahan fisik yang sangat prinsipal yang selalu terjadi dalam bahan pangan beku dan mempunyai efek terhadap sisfat-sifat kimia dan biokimia bahan pangan beku. Migrasi uap air dapat terjadi melalui proses sublimasi, absorbsi dan redistribusi uap air dalam bahan pangan atau komponen-komponen bahan pangan, rekristalisasi es dan kehilangan selama proses thawing. Migrasi uap air selama penyimpanan harus dihindarkan, karena menyebabkan berbagai kerugian dari dalam bahan beku, antara lain, terjadinya freezer burn , penampakan glassy pada produk pangan sehingga tampak tidak menarik, formasi pembentukan es yang tidak menarik di bagian kulit luar produk, hilangnya zat gizi dari dalam bahan pangan; tekstur; bahan yang jelek; kehilangan berat.
Sebaliknya pada kasus lain, kehilangan uap air dari produk justru menguntungkan bagi kualitas dan keamanan produk. Selama proses pembekuan. migrasi uap air dapat mencegah pertumbuhan mikrobilogi yang merugikan karena penurunan aktivitas air. Penyerapan uap air oleh bahan pangan dan redistribusi di antara komponen bahan pangan diharapkan pada proses pembekuan pie atau pizza, karena dihasilkan produk kering dan renyah. Rekristalisasi adalah proses pembesaran kristal kecil menjadi besar. Pengaruh rekristalisasi lebih diharapkan bagi konsumen es krim yang ingin menyimpan kembali es krim untuk beberapa lama.
Perubahan Fase dan Formasi Kristal Es
Ketika temperatur produk makanan diturunkan hingga di bawah titik beku air, air mulai membentuk kristal es. Pembentukan kristal es dapat disebabkan oleh kombinasi molekul-molekul air yang disebut dengan nukleasi homogenik, atau pembentukan inti di sekitar partikel tersuspensi yang dikenal dengan nama nukleasi heterogen. Nukleasi homogen terjadi dalam kondisi di mana zat terbebas dari zat pengotor yang pada umumnya berperan sebagai inti ketika terjadi proses pembekuan. Nukleasi heterogen terjadi ketika molekul-molekul air bersatu dengan agen nukleasi seperti benda asing, zat tak terlarut, atau bahkan dinding pembungkus.[ Nukleasi heterogen adalah tipe yang umum terjadi dalam proses pembekuan makanan.
Tipe ketiga dari proses nukleasi, yang disebut dengan pembentukan inti sekunder, terbentuk ketika kristal-kristal membelah. Tipe kristalisasi ini memberikan ukuran kristal yang seragam, dan umum terjadi pada proses pembekuan makanan cair (Franks, 1987). Umumnya, dalam proses pembekuan makanan, temperatur berkurang mulai dari temperatur awal di atas titik beku hingga beberapa derajat di bawah titik beku. Dalam proses ini, temperatur di 0 hingga -5oC disebut zona kritis yang diperlukan oleh makanan dalam pembentukan kristal-kristal es. Lamanya waktu yang diperlukan bagi makanan dalam melalui zona kritis ini menentukan jumlah dan ukuran kristal es yang terbentuk. Proses pembekuan yang cepat akan membentuk sejumlah besar kristal es berukuran kecil, sedangkan pendinginan dalam waktu yang lambat akan membentuk sejumlah kecil kristal es berukuran besar. Pembekuan yang lambat memberikan waktu bagi molekul-molekul air untuk bermigrasi menuju inti yang akan bersatu dengannya untuk membentuk agregat kristal es sehingga menghasilkan kristal es berukuran besar. Pembentukan kristal es berukuran besar ini akan memengaruhi struktur makanan dan menyebabkan hilangnya kualitas makanan. Kristal es yang besar akan menusuk dinding sel produk makanan dan merusaknya. Kerusakan akan semakin besar dengan semakin lambatnya laju pembekuan. Solusi terbaik adalah dengan mencegah terjadinya kristalisasi ini dengan risiko meningkatkan pertumbuhan mikroorganisme yang dapat merusak makanan karena temperatur yang masih memungkinkan bagi pertumbuhan mikroorganisme. Solusi dari masalah tersebut adalah dengan menambahkan protein anti beku yang dapat menurunkan titik beku air dan mencegah kristalisasi pada temperatur yang sangat rendah.
Sumber:




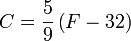 dan
dan 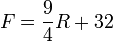 .
.


 .............................................................................................(12-8)
.............................................................................................(12-8)  ..............................................................................................(12-10)
..............................................................................................(12-10)  ........................................................................................(12-11)
........................................................................................(12-11)  ..........................................................................................................(12-12)
..........................................................................................................(12-12)  ...........................................................................(12-17)
...........................................................................(12-17)  .............................................................................(12-23)
.............................................................................(12-23)  .....................................................................(12-25)
.....................................................................(12-25)